Оптимальный масштаб для астрофото

Не так давно я решил разобраться для себя в сложном вопросе о связи оптического разрешения телескопа/атмосферы с тем, что получается на выходе в виде цифрового изображения матрицы. По этому поводу существует много статей, где даже приводятся формулы расчета по которым можно определить какая матрица наиболее оптимально подходит под конкретный телескоп. Правда есть два больших «но».

Первое «но» — существует завязка на состояние атмосферы, т.н. Seeing («сиинг»), который напрямую зависит от текущей турбулентности и выражается в угловых секундах разрешающей способности.

Второе — что делать тем, кто не может изменить параметры телескопа и астрокамеры? Ну вот есть текущая конфигурация и всё... Рассчитывай, не рассчитывай, толку от этого всё равно ноль — мы получим ровно то, на что способно данное оборудование.

Из меня математик/физик/оптик так себе, :-) поэтому я для себя я «нарисовал» простую картинку, чтобы было понятно.

Итак, у нас есть некая звезда, достаточно слабая, где-то на пределе фиксации телескопа/матрицы. Физически у неё есть угловые размеры, например 0.1" (почти точка, все цифры условные) на околоземной орбите. Свет от звезды проходит через атмосферу, которая в зависимости от турбулентности (параметр seeing) «разбалтывает» её до 2". Дальше свет попадает в оптику телескопа, который за счет Диска Эйри (и качества оптики) еще больше увеличивает угловой размер, например до 3".

Следует отметить, что размер будет зависеть сразу от многих факторов, начиная от состояния атмосферы, оптикой телескопа и заканчивая видом растяжек вторички.

Дальше свет попадает на матрицу и диск звезды уже приобретает линейные размеры, например 0,1мм (напомню, цифры условны). То есть на этом уровне произошло «преобразование» углового размера звезды в линейный.

Матрица имеет своё разрешение, которое напрямую зависит от размера её пикселей. Очевидно, что чем более мелкий пиксель у матрицы, тем более детальным получится изображение звезды. И наоборот, если линейный размер звезды оказался меньше размера пикселя, то звезда как бы «проваливается» в пиксель и диск звезды превращается в «квадрат» — разрешения матрицы физически не достаточно, чтобы сформировать диск.

Но это ещё не всё. Физический пиксель матрицы соответствует (я опускаю внутреннюю «кухню» матриц) одному пикселю на итоговом цифровом изображении. Таким образом угловой размер звезды в итоге «преобразовался» в «мониторные» пиксели (px), например в 5px (диаметр).

При обработке изображения, как правило, размер звёзд хотят немного уменьшить. И если с большими и средними звездами проблем нет, то что делать с самыми мелкими? Ведь у них не только малый размер, но и небольшая яркость и контраст.

Самым простым решением будет — уменьшение масштаба изображения так, чтобы «распухшие» мелкие звёзды уменьшились в размере до приемлемого вида. Но как это определить?

Существует параметр FWHM (полуширина) (Full-Width Half-Maximum), но не для сиинга в угловых секундах, а для мелких звезд на конечном изображения в пикселях.

Определить FWHM несложно. Самый простой способ — это открыть изображение в фотошопе и простым выделением посмотреть размер какой-то мелкой звезды.

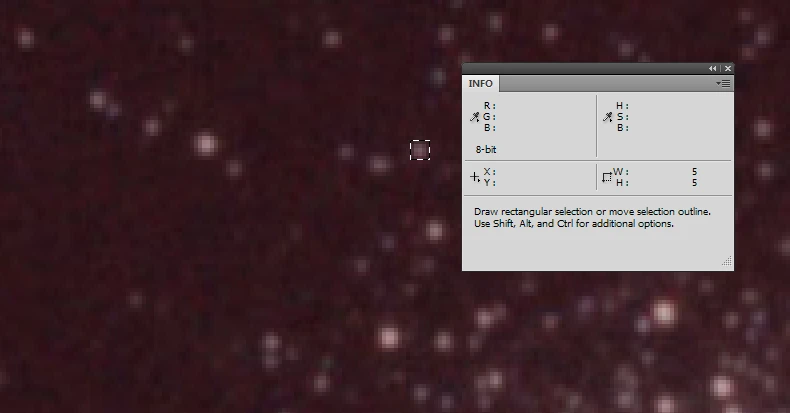
В данном примере это 5px. Второй способ воспользоваться какой-то астропрограммой, которая это умеет делать, например DeepSkyStacker. Нужно загрузить изображение и выбрать команду «Регистрация выбранных кадров». Нужно подобрать уровень определения звезд так, чтобы количество звезд оказалось достаточно большим — в этом случае программа будет искать мелкие звезды.

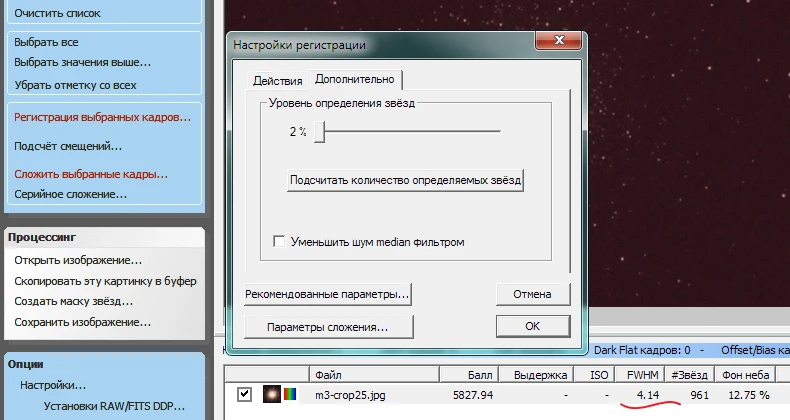
В данном примере размер оказался примерно таким же около 4px.

То есть на изображении, нет объектов менее этого размера, хотя в теории самые мелкие звезды должны иметь меньший размер. Насколько?

В этом вопросе очевидно только то, что минимальный размер — это 2px (речь о диаметре), иначе звезда превратится в точку. Чтобы обеспечить нормальное сглаживание краёв диска, значение следует увеличить хотя бы до 3px. Дальше несложная пропорция показывает, что масштаб следует уменьшить до 75% — в этом случае звезды 4..5px уменьшатся примерно до 3px.

На этой сравнительной картинке слева масштаб 100%, справа — 75% одного и того же объекта (M3 сразу после сложения). Теперь сделайте паузу и внимательно рассмотрите эту картинку: обратите внимание, что все мелкие звёзды при 75% никуда не исчезли.

Все операции по масштабирования я выполнял в фотошопе с помощью команды Image Size.

Таким образом мы можем сделать вывод, что текущая конфигурация телескоп+матрица даёт несколько завышенный масштаб. Это как сродни увеличению, когда мы хотим просто приблизить изображение для просмотра. Детализация при этом остается ровно той же.

Доказать это легко. Если теперь взять 75% изображение и опять его увеличить до исходных 100%, то мы получим почти туже самую картинку (слева тоже самое исходное, справа преобразование с 75% до 100%):

Если бы мы уменьшили масштаб например до 50%, то это привело бы к потере некоторых мелких звёзд, поскольку их размер уменьшился до 1..2px. Обратное увеличение уже не позволило бы восстановить исходный вид (это уже будет зависеть от алгоритма преобразования Фотошопа). Но мы уменьшили на ту величину, которая не привела к потере детализации.

На 75%-изображении FWHM определяется как 3.62px (в DSS). В зависимости от своих предпочтений, можно подобрать масштаб таким, чтобы FWHM оказался либо больше, либо меньше. Чисто визуально, значение 3-4 выглядит оптимально. Но какой при этом будет масштаб изображения, зависит от конкретного телескопа, матрицы и состояния атмосферы. Чтобы это определить, придётся провести исследование по своим готовым снимкам.

Какие выводы можно сделать.

• Если на изображении большой FWHM, то есть смысл немного уменьшить масштаб изображения. Это уберёт излишнюю «пухлость» звезд.
• Детализация при этом практически не теряется.
• Если есть возможность, то лучше подобрать такую матрицу к телескопу, чтобы сразу получать приемлемый размер звёзд.